Kinematika Gerak Translasi Dan Rotasi

pada tanggal
KINEMATIKA GERAK TRANSLASI DAN ROTASI

 Gerak Translasi dan Rotasi

1.Gerak translasi

 Gerak Translasi adalah gerak suatu benda dimana setiap titik pada benda tersebut menempuh lintasandan bentuk yang sama. Lintasan pada gerak translasi dapat berupa garis lurus atau bukan. Hal ini terjadi karena syarat sebuah gerak translasi adalah “setiap titik pada benda tersebut menempuh lintasan dan bentuk yang sama”.

 Contoh gerak translasi : Gerak sebuah balok di atas suatu permukaan datar tanpa mengguling, darikedudukan 1 ke kedudukan 2 pada jarak yang sama yaitu,

Gambar 1.1 

 

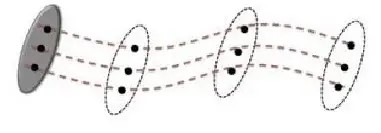
Gerak Translasi sebuah Balok Dengan Lintasan LurusGambar 1.2 di bawah ini juga menunjukan gerak translasi, meskipun pada lintasan melengkung, tetapibentuk dan panjang lintasan sama, dari kedudukan satu ke kedudukan lain.

                                                    gambar 1.2

2. Gerak Rotasi

 

Benda disebut melakukan gerak rotasi jika setiap titik pada benda itu, kecuali titik-titik padasumbu putar menempuh lintasan berbentuk lingkaran (gambar 1.3). Sumbu Putar adalah suatu garislurus yang melalui pusat lingkaran dan tegak lurus pada bidang lingkaran.

Catatan : penyebab translasi adalah gaya, sedangkan penyebab gerak rotasi adalah momen gaya.

                                    

                                                        gambar 1.3


Jenis-Jenis Gerak Rotasi

Gerak Rotasi dibedakan menjadi tiga jenis.

  1. Gerak terhadap sumbu tetap : Dikenal juga sebagai rotasi murni dan menggambarkan rotasi suatu benda di sekitar titik tetap. Beberapa contohnya adalah perputaran bilah kipas atau perputaran jarum jam pada jam analog karena keduanya berputar pada suatu titik tetap di pusat.
  2. Kombinasi gerak rotasi dan translasi . Gerak ini menggambarkan suatu benda, yang komponen-komponennya dapat berputar pada suatu titik tetap, sedangkan benda itu sendiri bergerak sepanjang lintasan linier. Contohnya adalah roda yang menggelinding pada mobil. Roda mempunyai dua kecepatan, satu akibat putaran roda dan satu lagi akibat gerak translasi mobil.
  3. Rotasi terhadap sumbu rotasi. Gerak ini menggambarkan benda yang berputar pada suatu sumbu sekaligus juga berputar mengelilingi benda lain. Contohnya adalah bumi yang mengorbit mengelilingi matahari dan juga berputar pada porosnya.

Kinematika Gerak Rotasi

Besaran rotasi seperti sudut θ , kecepatan sudut ω , dan percepatan sudut α . Mari kita lihat bagaimana persamaan gerak berhubungan dengan persamaan gerak rotasi. Bayangkan sebuah roda yang mulai berputar dengan percepatan sudut dan menempuh banyak putaran. Dari segi notasi formal dapat dikatakan bahwa roda yang mempunyai  α besar akhirnya berputar dengan sudut yang besar melalui beberapa putaran ( θ) . Situasi ini mirip dengan kendaraan yang bergerak di jalan dengan percepatan tertentu dan mencapai kecepatan tertentu. Parameter ini dapat dihitung dengan menggunakan kinematika gerak linier. Pendekatan serupa dapat digunakan dalam gerakan rotasi. Persamaan ini disebut persamaan kinematik gerak rotasi. Tabel di bawah menunjukkan beberapa besaran analog. 

Rotasi Terjemahan
ωay
θ S
αA
θ = ωts = vt

Persamaan Gerak Kinematik

Untuk benda yang bergerak dengan percepatan “a”. Katakanlah waktu dilambangkan dengan “t”, kecepatan sekarang dengan “v”, kecepatan awal dengan “u” dan jarak yang ditempuh benda dengan “s”. Persamaan yang mengatur gerak ini diberikan di bawah ini. Ingatlah bahwa persamaan ini hanya untuk situasi di mana percepatan “a” konstan dan benda bergerak lurus. 

  1. v = kamu + pada
  2. s = ut + \frac{1}{2}at^2
  3. v 2 = kamu 2 + 2as

Sekarang, dalam kasus gerak rotasi, kecepatan (v) sama dengan kecepatan sudut ( ω ). Perpindahan “s” dianalogikan dengan sudut rotasi ( θ ), percepatan (a) dianalogikan dengan percepatan sudut ( α ). 

Persamaan Kinematik Gerak Rotasi

Untuk benda yang berputar dengan percepatan sudut  α. Katakanlah waktu dinotasikan dengan “t”, kecepatan sudut saat ini dengan  ω , kecepatan awal sebesar , dan sudut yang ditempuh benda dengan  θ . Persamaan yang mengatur gerak ini diberikan di bawah ini. Ingatlah bahwa persamaan ini hanya untuk situasi dimana percepatan sudutnya konstan. 

  1. \omega = \omega_o + \alpha t
  2. \theta = \omega_ot + \frac{1}{2}\alpha t^2
  3. \omega^2 = \omega_o^2 + 2\alfa\theta

Contoh;

1.Jika sebuah benda berputar dengan kecepatan sudut 15rad/s, berapakah perpindahan sudutnya dalam 5 sekon? 

Menjawab: 

Misalkan  \omega_o kecepatan sudut awal dilambangkan.

Diberikan: \omega_o = 15 \teks{ rad/s}

Tujuannya adalah untuk mencari perpindahan sudut \theta

\theta = \omega.t \\ = \theta = (15)(5) \\ = \theta = 75 \text{ rad.}

2. Jika sebuah benda berputar dengan percepatan 2 radian/s 2 . Jika kecepatan sudut awal adalah 15rad/s, berapakah kecepatan sudut dalam waktu 5 sekon? 

Menjawab: 

Misalkan  \omega_o kecepatan sudut awal dan  \akhir kecepatan sudut akhir. 

Diketahui:  \omega_o = 15,  \alfa = 2 radian/s 2

Untuk mengetahui nilai “v” dapat digunakan persamaan gerak pertama. 

\omega = \omega_o + \alpha t

Memasukkan nilai dalam persamaan ini, 

\omega = \omega_o + \alpha t \\ = \omega = 15 + (2)(5) \\ = \omega = 15 + (10) \\ = \omega = 25 \text{ rad/s}



referensi;

https://id.scribd.com/document/364665844/1-Materi-Mekanika-Gerak-Translasi-Dan-Rotasi

https://www.studysmarter.co.uk/explanations/physics/kinematics-physics/rotational-motion/

https://www.geeksforgeeks.org/kinematics-of-rotational-motion/

Komentar

Posting Komentar